【搬运】后缀自动机

前言

本文参考WC2012陈立杰论文，在其基础上作总结与扩展。

简介

后缀自动机（Suffix Automaton，下简称SAM），是可以识别字符串 $S$ 的所有后缀的有限状态自动机。它也可以用来识别字符串 $S$ 的所有子串，处理许多字符串的问题。

有限状态自动机

有限状态自动机是一种用于识别字符串的模型。

自动机由五个部分组成， $alpha$ ：字符集， $state$ ：状态集合， $init$ ：初始状态， $end$ ：结束状态集合， $trans$ ：状态转移函数。

对于自动机 $A$ ，若 $S\in end$ ，则称 $A$ 能识别字符串 $S$ ，记 $A(S)=true$ ，否则 $A(S)=false$ 。

设 $trans(s,ch)$ 表示当前状态 $s$ ，在读入字符 $ch$ 之后，所到达的状态。

那么自动机识别一个字符串 $S$ 的过程是：从初始状态 $init$ 开始，对 $S$ 的每个字符 $ch$ 依次执行状态转移 $trans(cur,ch)$ ，最终的状态 $t$ 就是 $S$ 所在的状态。

设 $trans(init,S)$ 表示从 $init$ 开始，在读入字符串 $S$ 之后，所到达的状态。

字符串 $S$ 的后缀自动机需要满足的，就是 $A(trans(init,str))=true$ 当且仅当 $str$ 是 $S$ 的后缀，也就是A能且只能识别 $S$ 的后缀。

SAM与后缀树

事实上，SAM并没有那么抽象或遥不可及。我们熟悉的后缀树就是SAM最简单的实现。

对于字符串aabbabd，建立它的后缀树：

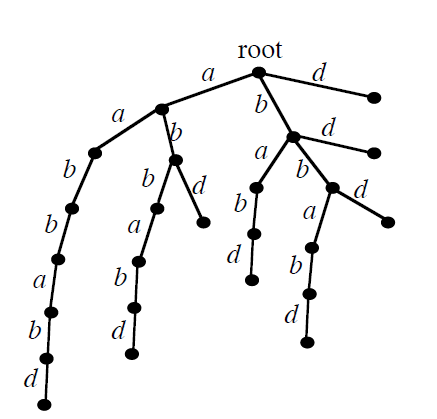
我们可以把它看成一个SAM：状态集合是树上所有点，初始状态是 $root$ ，状态转移函数是树的边，结束状态是叶子节点。因为后缀树的叶子节点表示的正是字符串的所有后缀，所以后缀树就是一个SAM。

但这样实现的问题在于：时空复杂度过大。尽管后缀树有各种优化，但优化的效果仍不理想，不能达到线性的复杂度，而且代码繁难。

最简状态自动机

最简状态自动机，是指状态数最少的自动机。

通过下文要讲的状态的合并，可以将SAM的状态数优化到 $O(n)$ ，得到最简状态SAM。我们平常使用的SAM，就是最简状态SAM。

SAM上的状态

在讲状态合并之前，首先要明确SAM上应该有哪些状态。

记 $ST(str)=trans(init,str)$ ，即从初始状态开始，读入字符串 $str$ 后，所到达的状态。

记字符串 $S$ 的子串集合为 $Fac(S)$ 。

在刚才用后缀树实现的SAM上，状态集合是 $\{ST(str)\mid str\in Fac(S)\}$ ，其实对于SAM的所有实现都是这样。

因为，SAM的功能是识别 $S$ 的所有后缀。则SAM上保留的状态，应该是所有有潜力成为后缀（即再读入几个字符就成为后缀）的子串。那么，就应该保留 $S$ 的后缀的所有前缀，即 $S$ 的所有子串 $Fac(S)$ 。

形式化地， $ST(str)\neq null$ 当且仅当 $str\in Fac(S)$ 。

此时，原串的每个子串对应着一个状态，这就使状态数具有 $O(n^2)$ 的数量级，这是非常不妙的。于是，我们来考虑一下如何对这些状态进行合并。

状态的合并

考虑一下，对于一个状态，我们关心什么。

SAM的最终目的是识别后缀。所以对于一个状态，我们唯一关心的是，它能够识别哪些串。

回顾一下识别的定义： $ST(a)$ 能识别字符串 $b$ ，当且仅当 $ab\in Suf$ （ $ab$ 是字符串 $a$ 和 $b$ 连接， $Suf$ 是后缀集合）。

那么，可以得到 $b\in Suf$ 。

设 $a$ 在原串 $S$ 中出现的位置为 $\{[l_1,r_1],[l_2,r_2],\dots,[l_k,r_k]\}$ 。那么， $ST(a)$ 能识别的字符串 $b\in\{[r_1+1,n],[r_2+1,n],\dots,[r_k+1,n]\}$ （ $n$ 是 $S$ 的长度）。

可以发现，可识别的串与 $l$ 无关，只与 $r$ 有关。换句话说，对于一个状态，我们只关心 $r$ 。

重要定义： $Right(a)=\{r_1,r_2,\dots,r_k\}$ （即 $a$ 在 $S$ 中出现位置的右端点集合）。

那么，对于一个状态，我们只需要关心 $Right$ 集合即可。这就意味着：

$Right$ 集合相同的状态，都可以被合并成一个。

所以，一个状态 $s$ ，由所有 $Right$ 集合是 $Right(s)$ 的字符串组成。

如此合并之后，状态数就大大减小了。事实上，状态数已经减小到了 $O(n)$ 。至于证明，下面会提到。

状态对应的字符串

刚才说了，状态 $s$ 由所有 $Right$ 集合是 $Right(s)$ 的字符串组成。那么，如何确定这些字符串呢？

设 $r\in Right(s)$ ，事实上，只要给出串长度 $len$ ，就可以确定一个串 $[r-len+1,r]$ 。

对于状态 $s$ ，只有一些符合条件的 $len$ ，才能使得到的串 $str=[r-len+1,r]$ 属于状态 $s$ ，也就是使得 $Right(str)=Right(s)$ 。

易证，若长度 $l$ 和 $r$ 都合法，那么 $len\in[l,r]$ 都合法。也就是说，合法长度是一段区间。

一个定义：状态 $s$ 和合法长度区间记为 $[Min(s),Max(s)]$ 。

Right集合之间的关系

结论：任意两个状态的 $Right$ 集合，要么不相交，要么一个是另一个的真子集。

这个结论非常重要，是SAM可以达到线性复杂度的基础。

证明如下：

设两个状态为 $a,b$ ， $Right$ 集合为 $R_a,R_b$ 。

设 $R_a$ 和 $R_b$ 相交，取 $r\in R_a\cap R_b$ 。

由于 $a,b$ 对应的串不可能有交集，则 $[Min(a),Max(a)]$ 和 $[Min(b),Max(b)]$ 也不会有交集。不妨设 $Max(a)<Min(b)$ 。

那么，由于都是从 $r$ 往前，而且 $a$ 中的串更短，则 $a$ 中所有串都是 $b$ 中所有串的后缀。

这就意味着， $b$ 中的串出现的位置， $a$ 中的串也必然出现了，即 $R_b\subseteq R_a$ 。

又因为两个状态 $Right$ 集合不可能相同，则 $R_b\subsetneq R_a$ ，结论得证。

parent树

从上述结论可以发现， $Right$ 集合构成了一个树形结构，我们称之为parent树。

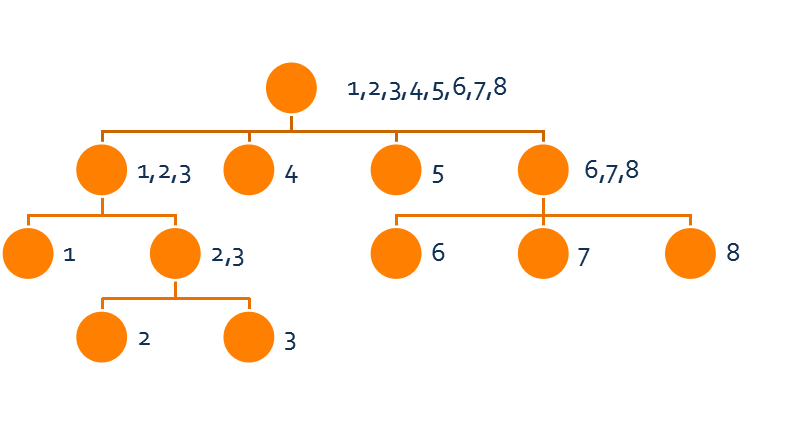
那么，通过“父子真包含”和“兄弟不相交”这两个性质，容易证明结点个数为 $O(n)$ ，也就是说SAM的空间复杂度是线性的。

实际上，parent树上儿子与父亲的合法长度区间 $[Min(s),Max(s)]$ 也有着联系：

设状态 $s$ 在parent树上的父亲是 $fa$ ， $s$ 的合法长度区间为 $[Min(s),Max(s)]$ 。

考虑长度 $Min(s)-1$ 对应的串 $str$ ，它不在状态 $s$ 中，说明随着串变短，出现的位置越来越多， $Right(str)$ 已经超出了 $Right(s)$ 的范围，即 $Right(str)$ 包含 $Right(s)$ ，而且是包含 $Right(s)$ 的集合中最小的一个。

根据parent树的定义， $str$ 一定属于状态 $fa$ ，那么 $Min(s)-1<=Max(fa)$ 。

又因为 $Right(s)$ 与 $Right(fa)$ 有交集，那么合法长度就不能有交集（不然会有同时处于两个状态的串）。所以 $Min(s)>Max(fa)$ 。

综上： $Max(fa)=Min(s)-1$ 。

Right集合的存储

SAM上的每个状态，都有一个对应的 $Right$ 集合。如果暴力存储每个状态的 $Right$ 集合，空间将是 $O(n\log n)$ 的。但如果利用我们利用parent树的一些性质，就可以不必直接存储每个结点的 $Right$ 集合。

如果按照上面那张图，可以发现在parent树上，一个结点的 $Right$ 集合是其所有子结点的 $Right$ 集合的并集。

那么，一个结点的 $Right$ 集合，就可以通过遍历其子树上的叶子节点得到，不必直接存储。

如果得到了某个串的 $Right$ 集合大小，就可以求出它在原串中出现了几次，这是 $Right$ 集合最经典的用法。当然这些都是后话。

错误纠正

（以下内容陈立杰论文中没有提到，不保证正确性，请带着批判的眼光阅读~~或跳过它也没有什么影响~~）。

回到这张图。这张图过于理想了，很容易误导人，使人感觉parent树的长相都这么好看。事实上，真正的parent树并不太可能长得这么可爱。

首先，Right集合里的元素并不一定是 $\{1,2,3\}$ 这样连续的，仍然存在 $\{2,5,7\}$ 这样的集合。

还有一点，就是刚才说的“在parent树上，一个结点的 $Right$ 集合是其所有子结点的 $Right$ 集合的并集。”这句话是错的。

以字符串aa为例，它有两个子串：a、aa，对应的 $Right$ 集合分别为 $\{1,2\},\{2\}$ 。而 $\{1,2\}$ 在parent树上有且只有 $\{2\}$ 这个子结点，元素 $1$ 缺失了，显然不符合上述结论。

我们来分析一下“缺失元素”的本质。设当前状态为 $s$ ，缺失元素为 $r$ 。

缺失元素 $r$ ，本质就是不存在 $Right$ 集合为 $\{r\}$ 的串。这意味着什么呢？

我们假设存在 $Right$ 集合为 $\{r\}$ 的状态，那么它一定是 $s$ 的儿子，我们把它记为 $son$ 。根据前面说的parent树的性质， $son$ 状态的合法长度区间为 $[Max(s)+1,r]$ 。而状态 $son$ 不存在，说明 $Max(s)+1>r$ 。对于状态 $s$ ，显然有 $Max(s)<=r$ ，于是可得：

状态 $s$ 缺失元素 $r$ ，当且仅当 $Max(s)=r$ 。

由此，我们可以得到“缺失元素”这种情况的一个限制：对于状态 $s$ ，若其缺失元素，只会缺失 $Right(s)$ 中最小的 $r$ 。

证明：

若 $s$ 缺失两个或两个以上元素，则 $Max(s)=r_1,Max(s)=r_2,\dots$ 相互矛盾。

若 $s$ 缺失的元素不为最小，设缺失元素 $r$ ，最小元素为 $r_0$ 。因为 $Max(s)=r$ ，而 $Max(s)\le r_0$ ，得到 $r\le r_0$ ，矛盾。

故：对于状态 $s$ ，若其缺失元素，只会缺失 $Right(s)$ 中最小的元素 $r$ 。

所以，缺失元素并不会干扰我们之前的复杂度证明。若一个状态缺失元素 $r$ ，我们只要把缺失的 $\{r\}$ 人为补上，就可以得到理想的parent树，上面的证明仍然有效。而补的个数也是 $O(n)$ 的。

至于 $Right$ 集合的存储，就要做一些改动：

对于元素 $r$ ，若存在 $Right(a)=\{r\}$ ，则把元素 $r$ 放在 $a$ 上。否则，设状态 $b$ 缺失元素 $r$ ，则把元素 $r$ 放在 $b$ 上。求 $Right$ 集合时，只要把子树上放的元素并起来即可。

例如字符串aa，只有状态 $\{1,2\}$ 和 $\{2\}$ 。所以把元素 $1$ 放在 $\{1,2\}$ 上，把元素 $2$ 放在 $\{2\}$ 上。求 $Right$ 时只要求子树上元素构成的集合即可。

线性构造算法

经历了艰难的理解过程，终于要进入正题了：SAM的线性构造算法。

在此之前，先明确一点：前文讲的parent树，和SAM的真实结构是两个东西。parent树只是用来辅助构造SAM的。

本文介绍的SAM构造算法是在线算法，也就是从左到右把字符串中的字符一个个加入SAM。

设当前串为 $T$ ， $T$ 的长度为 $L$ ，要加入的字符为 $x$ 。

首先，考虑加入 $x$ 会影响哪些状态。

加入 $x$ 后，新增了若干个子串，这些子串都属于 $Suf(Tx)$ （ $Tx$ 的后缀）。那么 $Suf(Tx)$ 对应的状态都要被改动。

另外，考虑哪些串会转移到 $Suf(Tx)$ ：显然只有 $Suf(T)$ 通过 $trans(x)$ 会转移到 $Suf(Tx)$ 。所以 $Suf(T)$ 对应的转移函数都需要修改。

于是得出结论：添加字符 $x$ ，需要改动的状态为 $Suf(T)$ 和 $Suf(Tx)$ 。而 $Suf(Tx)$ 可以通过 $trans(Suf(T),x)$ 得到。所以我们只需要枚举 $Suf(T)$ 。

设 $Suf(T)$ 对应的状态（即 $Right$ 集合中包含 $L$ 的状态）为 $\{v_1,v_2,\dots,v_k\}$ 。那么，如何得到这些状态呢？

由于此时必定存在 $Right$ 集合为 $\{L\}$ 的状态（串 $T$ 对应的状态），设这个状态为 $p$ 。那么由于parent树的性质，所有的 $v$ 都是 $p$ 的祖先，可以利用Parent函数（ $Parent(s)$ 为 $s$ 在parent树上的父亲）得到它们。

不妨把所有 $v$ 从后代到祖先排为 $v_1=p,v_2,\dots,v_k=root$ 。另外，新建状态 $np=ST(Tx)$ ，则 $Right(np)=\{L+1\}$ 。

下面要做的事情，就是把状态 $np$ 插到SAM里去，并且修改 $ST(Suf(T))$ （就是所有 $v_i$ ）的转移函数和 $ST(Suf(Tx))$ （就是 $trans(v_i,x)$ ）的 $Right$ 集合。

首先，从后代到祖先枚举 $v_i$ 。

上文说过，我们需要修改 $v_i$ 的转移函数，也就是 $trans(v_i,x)$ 。

设当前枚举的 $v$ 的 $Right$ 集合为 $\{r_1,r_2,\dots,r_k=L\}$ 。

考虑在后面添加字符 $x$ ，那么只有 $S[r_i+1]=x$ 的 $r_i$ 满足要求。

若 $trans(v,x)=null$ ，则说明 $v$ 中没有满足要求的 $r_i$ 。

但随着 $v_1,v_2,v_3,\dots$ 的 $Right$ 集合逐渐扩大，若 $v_i$ 中有满足要求的 $r$ ，则 $v_{i+1}$ 中也有。

所以， $trans(v,x)=null$ 的 $v$ 是从 $v_1$ 开始连续的一段。

一个结论：添加完字符 $x$ 后， $Right(trans(v,x))$ 一定包含 $L+1$ 。

因为根据定义，状态 $v$ 包含的其中一个串是 $T$ 的后缀，再添一个 $x$ 就变成了 $Tx$ 的后缀，对应的 $r=L+1$ 。

所以，对于这些原本 $trans(v,x)=null$ 的 $v$ ，显然修改完的 $Right(trans(v,x))=\{L+1\}$ ，也就是说 $trans(v,x)=np$ ，直接连边即可。

处理完 $trans(v_i,x)=null$ 的 $v_i$ ，我们枚举到了第一个 $trans(v_i,x)\ne null$ 的 $v_i$ ，称之为 $v_p$ 。

记 $trans(v_p,x)=q$ 。

添加完字符 $x$ 后， $Right(trans(v_p,x))$ 一定包含 $L+1$ ，看似可以把 $L+1$ 直接插入 $Right(q)$ 。但其实并不能这样做，以下是反例：

（第一行是 $v_p$ ，第二行是 $q$ ）。

可以看出，若把 $L+1$ 强行插入 $Right(q)$ ，则 $Max(q)$ 被 $r=L+1$ 的串所限只能取到 $Max(v_p)+1=6$ ，而原来 $Max(q)=7$ 。 $Max(q)$ 的缩短将会导致一系列问题，所以我们不能这么做。

（不过如果 $Max(q)$ 本来就等于 $Max(v_p)+1$ ，则并不会出现什么问题。只需让 $Parent(np)=q$ ，相当于在 $Right(q)$ 中插入 $L+1$ ，就可以结束这个阶段了）。

此时，可以发现 $q$ 实际上被分成了两段：

（第一行是 $v_p$ ，第二、三行是被分成两段的 $q$ ）。

于是，我们新建结点 $nq$ ，使 $Right(nq)=Right(q)\cup\{L+1\}$ （对应图片第三行）。同时 $Max(nq)=Max(v_p)+1$ 。

为什么 $Max(nq)=Max(v_p)+1$ ？有没有可能更大？

实际上，因为 $v_p$ 的所有儿子都没有 $x$ 的转移边，这就说明比 $Max(v_p)$ 更长的 $T$ 的后缀再接上一个字符 $x$ 都是没有在 $T$ 中出现过的，也就是说它们在添加x之后的 $Right$ 集合一定是 $\{L+1\}$ ，那么就不会在 $nq$ 中。

先考虑 $np,q,nq$ 这些状态在parent树上的关系：

由于 $Right(q)\subsetneqq Right(nq)$ ，则： $Parent(q)=nq$ 。

同时 $Right(np)=\{L+1\}\subsetneqq Right(nq)$ ，则： $Parent(np)=nq$ 。

最后，把 $Parent(nq)$ 设为原来的 $Parent(q)$ 。为什么可以这么做？

因为 $q$ 表示的字符串中包含 $Tx$ 的后缀，设这个串为 $str$ ，结束位置为 $r$ 。 $Parent(q)$ 的 $Right$ 集合中肯定也包含 $r$ ，且从 $r$ 往前的串长度比 $q$ 短，这就意味着 $Parent(q)$ 中包含 $str$ 的后缀（ $str$ 的后缀同时也是 $Tx$ 的后缀）。进而 $Right(Parent(q))$ 就包含 $L+1$ 。

又因为 $Right(q)\subsetneqq Right(Parent(q))$ ，则 $Right(nq)=Right(q)\cup \{L+1\}\subsetneqq Right(Parent(q))$ ，即： $Parent(nq)=Parent(q)$ 。

总结步骤： $Parent(q)=Parent(np)=nq$ ， $Parent(nq)=原来的Parent(q)$ 。

处理完 $Parent$ 树上的连边，还要考虑SAM上的连边，也就是转移函数。

注意到在 $trans(nq,ch)$ 中， $nq$ 相比起 $q$ 多的结束位置 $L+1$ 是不起作用的（已经到末尾了没法再添字符）。所以 $nq$ 的转移函数直接从 $q$ 拷贝过来即可。

处理完 $v_p$ ，剩下的 $v_{p+1},\dots, v_k$ 的 $trans(x)$ 一定都不为空。并且，随着 $Right(v)$ 的变大， $Right(trans(v,x))$ 也会变大。那么只有一段 $v_p,\dots,v_e$ 的 $trans(v,x)=q$ 。因为 $q$ 已经被我们拆成了 $q$ 和 $nq$ ，且 $nq$ 包含 $\{L+1\}$ ，那么就应该把 $v_p,\dots,v_e$ 的 $trans(v,x)$ 都改为 $nq$ 。

至于 $v_e$ 以后的 $v$ ，就不用改动了。你可能会问，不应该在剩下的 $trans(v_i,x)$ 的Right集合中插入 $\{L+1\}$ 吗？

事实上，剩下的 $v_i$ 的 $trans(v_i,x)$ 一定是 $nq$ 的祖先，而刚才 $nq$ 中已经加入了 $L+1$ ，则 $trans(v_i,x)$ 中就也加入了 $L+1$ ，无需再改。

至此，算法结束。

步骤总结

设已经加入的串为 $T$ ，长度为 $L$ ，当前待添加字符为 $x$ 。

令 $p=ST(T)$ ，即 $Right$ 集合为 $\{L\}$ 的状态。

新建 $np=ST(Tx)$ ，即 $Right$ 集合为 $\{L+1\}$ 的状态。

对 $p$ 的所有 $trans(v,x)=null$ 的祖先 $v$ ， $trans(v,x)=np$ 。

令 $p$ 的第一个 $trans(v,x)!=null$ 的祖先为 $v_p$ 。若找不到这样的 $v_p$ 则 $Parent(np)=root$ 并退出。

记 $q=trans(v_p,x)$ 。若 $Max(q)=Max(v_p)+1$ ，则 $Parent(np)=q$ 并退出。

否则，新建结点 $nq$ ， $Parent(q)=Parent(np)=nq$ ， $Parent(nq)=原来的Parent(q)$ ，并且 $nq$ 的转移函数拷贝 $q$ 的。

对于所有为 $p$ 的祖先且满足 $trans(v,x)=q$ 的状态 $v$ ， $trans(v,x)=nq$ 。

代码

SAM主要难在理解，代码其实非常短。

void Extend(char c) {
    int x = c - 'a', p = last, np = last = ++top;
    mx[np] = mx[p] + 1; cnt[np] = 1;
    for (; p && !ch[p][x]; p = fa[p]) ch[p][x] = np;
    if (!p) { fa[np] = 1; return; }
    int q = ch[p][x];
    if (mx[q] == mx[p] + 1) { fa[np] = q; return; }
    int nq = ++top; mx[nq] = mx[p] + 1;
    fa[nq] = fa[q]; fa[q] = fa[np] = nq;
    memcpy(ch[nq], ch[q], sizeof(ch[q]));
    for (; ch[p][x] == q; p = fa[p]) ch[p][x] = nq;
}