平衡树-2：平衡树与区间操作

d0j1a_1701温馨提示：

这是一篇讲义，内容较优质，请放心食用。

前言

在上一篇文章中，我们已经学习了二叉查找树和Treap，现在我们来学习Splay和无旋Treap。

更多的平衡树

Splay

访问局部性原理：

  • 最近刚刚被访问过的节点极易被再次访问（时间局部性）
  • 最近刚刚被访问过的节点的相邻节点极易被访问（空间局部性）

Splay(伸展树)是另一种平衡树实现。

由 Daniel Sleator 和 Robert Tarjan 发明 (怎么又是你) 。

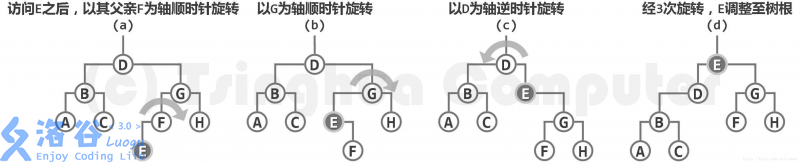
Splay根据访问局部性原理设计，这种平衡树在访问节点后将它放在距离根节点较近的位置以增加查找速度。

与Treap不同，Splay不需要实时保持全树平衡。它只需要在每次访问一个节点后将它旋转到根节点并在沿途的旋转操作中调整树高。

splay操作

splay是Splay树的一种特殊操作。（这句话区分大小写）

splay操作通过一系列旋转将一个节点移动到平衡树的根节点（或其他节点）。

为了将节点移动到根节点，我们需要记录每个结点的父节点，这意味着需要重写节点定义和旋转操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
struct Node {//节点定义 ch[0]为左孩子 ch[1]为右孩子 fa为父节点
	int ch[2], fa, val, sz, cnt;
} tree[100010];
int root, len;
inline int newNode(int val, int fa = 0) {
	return tree[++len] = {{0, 0}, fa, val, 1, 1}, len;
}
inline int getlr(int id) {//辅助函数 判断节点是父节点的左孩子还是右孩子 0为左 1为右
	return tree[tree[id].fa].ch[1] == id;
}
inline void pushup(int id) {
	tree[id].sz = tree[tree[id].ch[0]].sz + tree[tree[id].ch[1]].sz + tree[id].cnt;
}
inline void rotate(int id) {//将节点旋转到自己父节点的位置 左右旋转写在同一个函数中
	int fa = tree[id].fa, gf = tree[fa].fa, lr = getlr(id), ch = tree[id].ch[lr ^ 1];
    //fa 父节点 gf 祖父节点 lr 当前节点是左孩子还是右孩子 ch 当前节点另一边(如果当前节点是父节点的左孩子则是当前节点的右孩子，反之同理)的孩子
	tree[fa].ch[lr] = ch, tree[ch].fa = fa;//原父节点的孩子变成当前节点另一边的孩子，同时更新当前节点孩子的fa
	tree[gf].ch[getlr(fa)] = id, tree[id].fa = gf;//原祖父节点的孩子变成当前节点，同时更新当前节点的fa
	tree[id].ch[lr ^ 1] = fa, tree[fa].fa = id;//当前节点的孩子变成原父节点，同时更新原父节点的fa
	pushup(fa), pushup(id);//因为旋转后fa是id的子节点，所以先更新fa再更新id
}

逐层伸展(spaly)

图片来自Freddie的洛谷博客。

有了旋转操作，splay怎么实现就一目了然了。

逐层伸展

于是我们可以很容易的写出splay操作的代码：

1
2
3
4
5
//将节点旋转成goal的孩子,goal=0时旋转到根节点
inline void spaly(int id, int goal = 0) {
	while(tree[id].fa != goal)	rotate(id);
	if(!goal)	root = id;
}

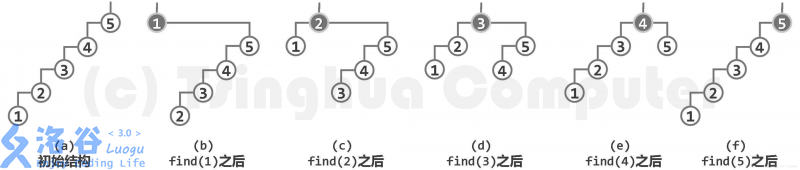
但这样做有一个致命的问题：可以被恶意构造的数据卡成 O(n)O(n) 。

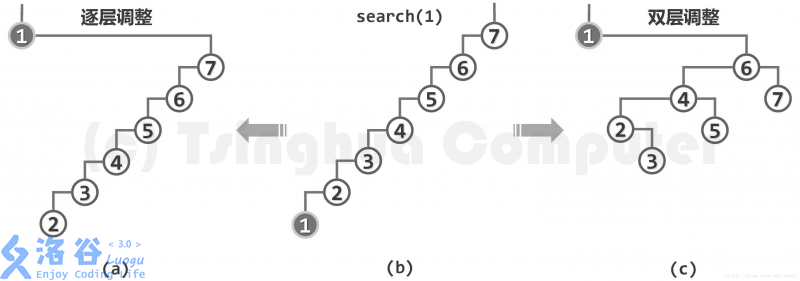
如图：

逐层伸展-危

可见只需要几个简单的单调数据就可以把平衡树卡成一叉查找链。

双层伸展(splay)

为了解决这个致命的问题，我们引入双层伸展。

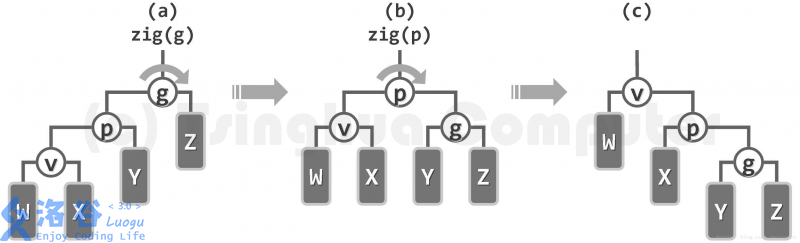
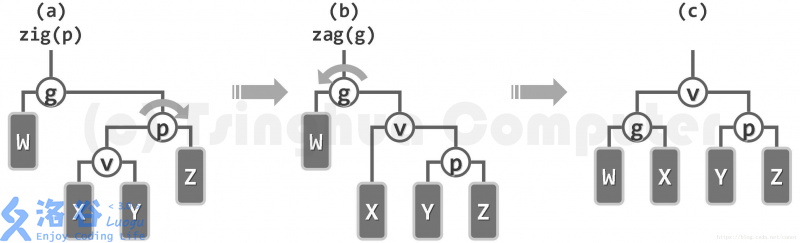
根据平衡树的结构，大致可将splay操作需要处理的类型分为两种。

zigzig/zagzag型

双旋-zigzig

当祖父节点，父亲节点与当前节点在同一条直线上时，先旋转父亲节点再旋转当前节点。

zigzag/zagzig型

双旋-情况2

当祖父节点，父亲节点与当前节点不在同一条直线上时，直接按照逐层伸展的方式处理即可。

这样即可得到双层伸展的splay操作：

1
2
3
4
5
6
7
8
9
10
11
inline void splay(int id, int goal = 0) {
	while(tree[id].fa != goal) {
		int fa = tree[id].fa, gf = tree[fa].fa;
		if(gf != goal) {
			if(getlr(id) == getlr(fa))	rotate(fa);//zigzig/zagzag
			else	rotate(id);//zigzag/zagzig
		}
		rotate(id);
	}
	if(!goal)	root = id;
}

对比一下逐层伸展和双层伸展：

双层伸展

可见双层伸展每次可让树高大致减少一半。

因此当毒瘤出题人试图去访问一条长链时，每次访问都会让树高减少一半。

虽然每次操作时间复杂度最差为 O(n)O(n) ，但Splay树的均摊复杂度为 O(n)+O(n/2)+O(n/4)+O(n/8)+...+O(1)=O(nlog⁡n)O(n) + O(n/2) + O(n/4) + O(n/8) + ... + O(1) = O(n \log n) 。

查找

由于在Splay中查找后会导致被查找结点旋转到根节点，所以Splay中查找是一个很有用的操作。

这个函数查找的是小于等于val的最大节点，如果val在平衡树中会被旋转到根节点，否则将val的前驱旋转到根节点。

1
2
3
4
5
6
7
int find(int val) {
	if(!root)	return -1;
	int p = root;
	while(tree[p].ch[tree[p].val < val] && tree[p].val != val)	p = tree[p].ch[tree[p].val < val];
	splay(p);//找到了就转到根节点
	return p;
}

前驱/后继

有了find函数后就十分容易实现。

查找前驱只需要find(x)后在根节点的左子树上找最大值（如果根节点就是x的前驱直接返回就好，否则左子树的最大值就是小于x的最大值，即为前驱）。

查找后继同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline int pre(int x) {
	find(x);
	if(tree[root].val < x)	return root;//如果根节点就是x的前驱那么直接返回
	int id = tree[root].ch[0];//根节点的左子树
	while(tree[id].ch[1])	id = tree[id].ch[1];//向右爬
	splay(id);//别忘了把被查找结点转上去
	return id;
}
inline int nxt(int x) {
	find(x);
	if(tree[root].val > x)	return root;
	int id = tree[root].ch[1];
	while(tree[id].ch[0])	id = tree[id].ch[0];
	splay(id);
	return id;
}

查排名

find(val)后全部比val小的节点都会在根节点的左子树上，所以只需要输出根节点左子树的大小+1即可。

1
2
3
4
inline int rnk(int val) {
	find(val);
	return tree[tree[root].ch[0]].sz + 1;
}

删除

显然，一个数的前驱和后继之间只可能有它自己。

1
2
3
4
5
6
7
8
9
void erase(int val) {
	int p = pre(val), q = nxt(val);//找前驱后继
	splay(p), splay(q, p);//把前驱转到根节点，后继转到前驱的(右)孩子
	int id = tree[q].ch[0];//此时后继的左孩子上即为大于前驱小于后继的节点，就是要删除的节点
	if(tree[id].cnt > 1)	tree[id].cnt--,tree[id].sz--, splay(id);//如果元素数量大于一就删掉一个然后转到根节点
	else tree[q].ch[0] = 0;//如果只剩下一个就直接扔掉就好了
	pushup(q);//别忘了更新
	pushup(p);
}

但是这样删除会出现问题：如果val的前驱或后继不存在整棵树会爆炸（把一个不存在的节点转到根节点？）。

因此需要在建树时插入两个值为 infinf 和 −inf-inf 的哨兵节点。相应的，kth操作和rnk操作也需要特殊的处理。

Splay树的其他操作和其他平衡树一致，只是别忘了在访问节点后进行splay操作。

给出普通平衡树的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <iostream>
using namespace std;
const int inf = 2147483647;
struct Node {
	int ch[2], fa, val, sz, cnt;
} tree[100010];
int root, len;
inline int newNode(int val, int fa = 0) {
	return tree[++len] = {{0, 0}, fa, val, 1, 1}, len;
}
inline int getlr(int id) {
	return tree[tree[id].fa].ch[1] == id;
}
inline void pushup(int id) {
	tree[id].sz = tree[tree[id].ch[0]].sz + tree[tree[id].ch[1]].sz + tree[id].cnt;
}
inline void rotate(int id) {
	int fa = tree[id].fa, gf = tree[fa].fa, lr = getlr(id), ch = tree[id].ch[lr ^ 1];
	tree[fa].ch[lr] = ch, tree[ch].fa = fa;
	tree[gf].ch[getlr(fa)] = id, tree[id].fa = gf;
	tree[id].ch[lr ^ 1] = fa, tree[fa].fa = id;
	pushup(fa), pushup(id);
}
inline void splay(int id, int goal = 0) {
	while(tree[id].fa != goal) {
		int fa = tree[id].fa, gf = tree[fa].fa;
		if(gf != goal) {
			if(getlr(id) == getlr(fa))	rotate(fa);
			else	rotate(id);
		}
		rotate(id);
	}
	if(!goal)	root = id;
}
int find(int val) {
	if(!root)	return -1;
	int p = root;
	while(tree[p].ch[tree[p].val < val] && tree[p].val != val)	p = tree[p].ch[tree[p].val < val];
	splay(p);
	return p;
}
void insert(int &id, int fa, int val) {
	if(!id) {
		splay(id = newNode(val, fa));
		return;
	}
	if(tree[id].val == val)	tree[id].cnt++, splay(id);
	else	insert(tree[id].ch[tree[id].val < val], id, val);
}
inline int rnk(int val) {
	find(val);
	return tree[tree[root].ch[0]].sz + 1;
}
int kth(int id, int k) {
	if(!id) return -1;
	if(k <= tree[tree[id].ch[0]].sz)  return kth(tree[id].ch[0], k);
	else if(k <= tree[tree[id].ch[0]].sz + tree[id].cnt)  return splay(id), tree[id].val;
	return kth(tree[id].ch[1], k - tree[id].sz + tree[tree[id].ch[1]].sz);
}
inline int pre(int x) {
	find(x);
	if(tree[root].val < x)	return root;
	int id = tree[root].ch[0];
	while(tree[id].ch[1])	id = tree[id].ch[1];
	splay(id);
	return id;
}
inline int nxt(int x) {
	find(x);
	if(tree[root].val > x)	return root;
	int id = tree[root].ch[1];
	while(tree[id].ch[0])	id = tree[id].ch[0];
	splay(id);
	return id;
}
void erase(int val) {
	int p = pre(val), q = nxt(val);
	splay(p), splay(q, p);
	int id = tree[q].ch[0];
	if(tree[id].cnt > 1)	tree[id].cnt--, tree[id].sz--, splay(id);
	else tree[q].ch[0] = 0;
	pushup(q);
	pushup(p);
}
int q;
int main() {
	insert(root, 0, inf), insert(root, 0, -inf);
	cin >> q;
	while(q--) {
		int op, x;
		cin >> op >> x;
		switch(op) {
			case 1:
				insert(root, 0, x);
				break;
			case 2:
				erase(x);
				break;
			case 3:
				cout << rnk(x) - 1 << endl;
				break;
			case 4:
				cout << kth(root, x + 1) << endl;
				break;
			case 5:
				cout << tree[pre(x)].val << endl;
				break;
			case 6:
				cout << tree[nxt(x)].val << endl;
				break;
		}
	}
	system("pause");
	return 0;
}

热知识：使用逐层伸展（即"单旋"，同样的，双层伸展称为"双旋"）的Splay树一般被称为Spaly。这个名字来源于luoguP3721 单旋。

在随机数据下单旋Splay的常数比双旋Splay小。（普通平衡树中无论吸不吸O2单旋都比双旋快 50−70ms50-70ms ）

无旋Treap

以上提到的所有平衡树都基于旋转操作维持平衡。有没有不需要旋转的平衡树呢？

无旋Treap(又名FHQ-Treap，因为发明者叫FHQ)是一种无需旋转即可实现的平衡树，它同时具有支持区间操作，可持久化，码量小的特点。

正如它的名字，无旋Treap首先是棵Treap。它的每个节点有val数据域和weight权值域。

不同于其他平衡树，无旋Treap的基本操作只有**分裂(Split)和合并(Merge)**操作。

分裂

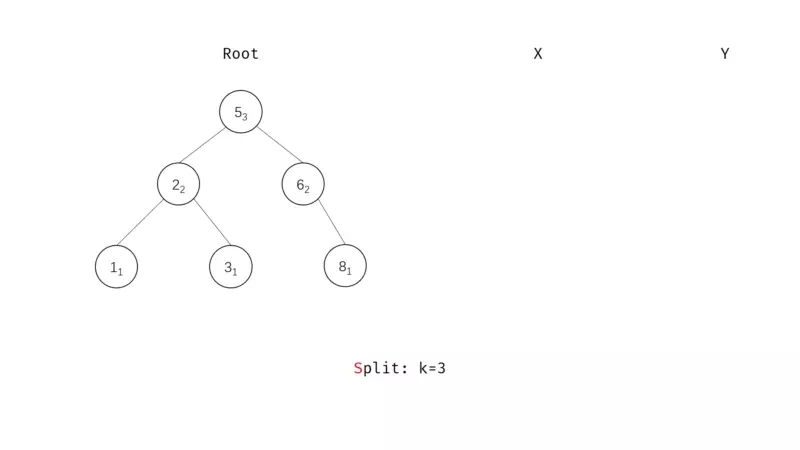
Split

这张图中的 k=3k=3 应为 k=2k=2 。(捂脸.jpg)

Split操作可将一棵Treap分裂为两棵Treap，一棵的全部节点 val≤kval\le k ，另一棵全部节点 val>kval>k 。

有一种简单的算法可以在 O(log⁡n)O(\log n) 的时间复杂度内进行分裂操作，代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void split(int id,int k,int &x,int &y) {//id为当前节点 x,y为当前分裂出的两棵Treap的子树根节点
	if(!id) {
		x = y = 0;//如果当前节点是空节点就返回
		return;
	}
	if(val[id]<=k) {
		x = id;//当前节点挂到x上
        //因为节点的左子树上的所有点小于等于当前节点，所以左子树上所有点都小于等于k
		split(rc[id],k,rc[id],y);//左子树上所有点挂在x上，向右子树分裂
	} else {
		y = id;//同理不解释
		split(lc[id],k,x,lc[id]);
	}
	updateSize(id);
}

合并

应该很好理解就不放动图了 实际上是我懒得做了

Merge操作可将两棵Treap合并为一棵Treap，需要满足第一棵Treap上全部节点小于等于第二棵树。

由于Treap是一个堆，merge时要将两个子树中weight较大的放在上面。

同样也可以在 O(log⁡n)O(\log n) 时间复杂度内进行，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
int merge(int x,int y) {
	if(!x||!y)	return x + y;//如果其中一棵树为空，则把另一棵树挂到当前节点上，如果两棵树都为空，当前节点就为空
	if(w[x]>w[y]) {//如果数据较小的那棵树当前节点权值大于另一棵树当前节点
         //因为x中所有节点小于y中任意节点 所以把x和x的左子树挂到当前节点上
		rc[x] = merge(rc[x],y);//向右继续合并
		updateSize(x);
		return x;//返回当前节点
	} else {
		lc[y] = merge(x,lc[y]);//同理不解释
		updateSize(y);
		return y;
	}
}

插入

这个时候，一定有人会说：

只会分裂和合并的平衡树我才不要！

但是有了这两个功能，就可以实现所有其他功能，并且代码量极少。

通过split操作可以将一个Treap分裂为两棵（分别是a: val≤xval \le x ,b: val>xval > x ）,我们只需要把一个新节点合并到a里面，再给两棵树合并到一起就完成了Insert操作。

1
2
3
4
5
void insert(int v) {
	int x,y;
	split(root,v,x,y);//root拆成两棵树
	root = merge(merge(x,newNode(v)),y);//合并
}

只用五行代码就实现了插入操作！

删除

只需要将一棵Treap分裂为三棵（分别是a: val<xval < x ,b: val=xval = x 与 c: val>xval > x）,我们只需要把b的两棵子树合并，再给两棵树合并到一起就完成了Insert操作。

1
2
3
4
5
void erase(int v) {
	int x,y,z;
	split(root,v,x,z),split(x,v-1,x,y);//root拆成[-inf,v),v,(v,inf]三棵树
	root = merge(merge(x,merge(lc[y],rc[y])),z);//合并
}

排名

rnk操作也很简单，把一棵Treap分裂成两棵（a: val≤xval\le x 与 b: val>xval>x ），此时size[a]就是比 xx 小的节点个数，排名就是size[a]+1。

1
2
3
4
5
6
7
int rnk(int v) {
	int x,y,res;
	split(root,v-1,x,y);
	res = sz[x] + 1;
	root = merge(x,y);
	return res;
}

前驱/后继

以前驱为例，所谓前驱就是比 xx 小的数中最大的，只需要分裂成 a: val<xval<x 与 b: val≥xval\ge x 两棵树然后找到a上的最大值即可，后继同理。

如何找一棵Treap上的最大值呢？只需要从根节点一直向右爬即可。找最小值就向左爬。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int pre(int v) {
	int x,y,p,res=-2147483647;
	split(root,v-1,x,y),p = x;
	while(p) res = val[p],p = rc[p];//从x开始向右爬
	root = merge(x,y);
	return res;
}
int nxt(int v) {
	int x,y,p,res=2147483647;
	split(root,v,x,y),p = y;
	while(p) res = val[p],p = lc[p];
	root = merge(x,y);
	return res;
}

其他操作

别忘了无旋Treap也是Treap，直接复制即可。

普通平衡树

我们再来切一下普通平衡树：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include <iostream>
#include <random>
using namespace std;
mt19937 mt(random_device {}());
int root = 0, len = 1, val[100010], lc[100010], rc[100010], sz[100010], w[100010];
inline int newNode(int v) {
	val[len] = v,sz[len] = 1,w[len] = mt(),lc[len] = rc[len] = 0;
    return len++;
}
inline void updateSize(int p) {
	sz[p] = sz[lc[p]] + sz[rc[p]] + 1;
}
void split(int id,int k,int &x,int &y) {
	if(!id) {
		x = y = 0;
		return;
	}
	if(val[id]<=k) x = id,split(rc[id],k,rc[id],y);
	else y = id,split(lc[id],k,x,lc[id]);
	updateSize(id);
}
int merge(int x,int y) {
	if(!x||!y)	return x + y;
	if(w[x]>w[y]) {
		rc[x] = merge(rc[x],y),updateSize(x);
		return x;
	} else {
		lc[y] = merge(x,lc[y]),updateSize(y);
		return y;
	}
}
void insert(int v) {
	int x,y;
	split(root,v,x,y);
	root = merge(merge(x,newNode(v)),y);
}
void erase(int v) {
	int x,y,z;
	split(root,v,x,z),split(x,v-1,x,y);
	root = merge(merge(x,merge(lc[y],rc[y])),z);
}
int rnk(int v) {
	int x,y,res;
	split(root,v-1,x,y);
	res = sz[x] + 1;
	root = merge(x,y);
	return res;
}
int kth(int k) {
	int p = root;
	while(1) {
		if(sz[lc[p]]+1==k)	return val[p];
		if(sz[lc[p]]>=k)	p = lc[p];
		else k -= sz[lc[p]] + 1,p = rc[p];
	}
	return val[p];
}
int pre(int v) {
	int x,y,p,res=-2147483647;
	split(root,v-1,x,y),p = x;
	while(p) res = val[p],p = rc[p];
	root = merge(x,y);
	return res;
}
int nxt(int v) {
	int x,y,p,res=2147483647;
	split(root,v,x,y),p = y;
	while(p) res = val[p],p = lc[p];
	root = merge(x,y);
	return res;
}
int main() {
	int n;
	cin >> n;
	while(n--) {
		int opt, x;
		cin >> opt >> x;
		switch(opt) {
			case 1:
				insert(x);
				break;
			case 2:
				erase(x);
				break;
			case 3:
				cout << rnk(x) << endl;
				break;
			case 4:
				cout << kth(x) << endl;
				break;
			case 5:
				cout << pre(x) << endl;
				break;
			case 6:
				cout << nxt(x) << endl;
				break;
		}
	}
	return 0;
}

关于常数

经过测试，普通平衡树中三种平衡树表现如下：

环境\时间\类型TreapSplay无旋Treap
洛谷 C++20 O2397ms454ms482ms
loj.ac C++20 O2266ms324ms292ms

什么？你说O2？€$₱都开O2了你确定你还不开？

多平台测试排除评测机波动等因素（loj.ac的评测机真的快），可以发现Splay和无旋Treap的常数类似，但均比Treap大。

原因很简单，Treap的操作只需要从上到下执行一次，而Splay需要在任意操作结束后进行splay操作向上旋转一次，无旋Treap需要多次split/merge才能完成一次操作。

但在实际测试中，无旋Treap的常数往往比Splay小~~(玄学？)~~，并且编码复杂度比Splay少上几倍，功能也丝毫不差，因此平常使用时一般使用无旋Treap。

区间操作

接下来到了重头戏——区间操作。本文关于区间操作的全部内容都使用无旋Treap。（当然Splay也可以实现，但它难写且常数比无旋Treap大，因此如果你想了解Splay区间操作请简单算法百度搜索深刻体会）

支持区间操作的平衡树可以实现线段树的全部功能，甚至还能实现区间插入等线段树没有的功能。

我们使用luoguP3372 模板:线段树1作为例题 (这是线段树的例题，所以我们不能使用线段树)

维护区间时，平衡树中维护的不是值，而是位置的大小关系。

如果你没能理解这点你在学习后面内容时就会脑短路。

节点声明

这道题要求你维护区间和，支持区间加。平衡树采用与线段树相同的方法实现区间操作：懒标记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int root, len, lc[100010], rc[100010], sz[100010], w[100010];//不解释
long long val[100010], sum[100010], add[100010];//sum: 当前子树所有节点和 add: 当前子树的加法懒标记
mt19937 mt(chrono::steady_clock::now().time_since_epoch().count());
inline int newNode(long long x) {
	++len, val[len] = sum[len] = x, lc[len] = rc[len] = add[len] = 0, sz[len] = 1, w[len] = mt();
    //不可写成val[++len] = sum[len]
	return len;
}
inline void pushup(int id) {
	sz[id] = sz[lc[id]] + sz[rc[id]] + 1;
	sum[id] = sum[lc[id]] + sum[rc[id]] + val[id];//维护sum
}
inline void pushdown(int id) {//标记下传
	if(!add[id])	return;//如果当前节点没有标记就不传
	if(lc[id])	val[lc[id]] += add[id], add[lc[id]] += add[id], sum[lc[id]] += sz[lc[id]] * add[id];//下传到左子树
	if(rc[id])	val[rc[id]] += add[id], add[rc[id]] += add[id], sum[rc[id]] += sz[rc[id]] * add[id];//下传到右子树
    //注意：修改sum值时增加的是子树大小*加法标记，因为sum是整个子树的和
	add[id] = 0;//清空
}

初始化区间

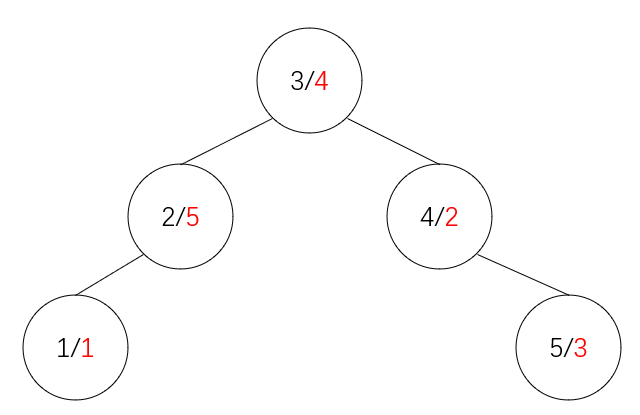
由于维护的是位置的大小关系，位置靠后的值一定大于位置靠前的值，我们只需要简单的把每一个值依次merge到无旋Treap里即可。

无旋Treap维护区间

这是merge完成后Treap可能的结构。

1
for(int i = 1; i <= n; i++)	cin >> x, root = merge(root, newNode(x));

分裂区间

为了更好的理解，在上一张图中我们把维护区间的平衡树视作以元素位置为关键字比较的平衡树。

但这个位置不一定要显式的表现（而且有的时候根本不能显式表现，比如需要进行动态插入或删除时）。观察这棵树可发现，每个元素在原数组中的位置就是它的排名rnk。为了更方便的分裂出一个区间，我们可以修改split函数为按排名分裂。

1
2
3
4
5
6
7
inline void split(int id, int k, int &x, int &y) {//分裂出两棵Treap x树中存储前k大的元素
	if(!id)	return x = y = 0, (void)0;
	pushdown(id);//如果需要用到懒标记就要把标记下传加在这里
	if(sz[lc[id]] + 1 <= k)	x = id, split(rc[id], k - sz[lc[id]] - 1, rc[id], y);//如果当前节点的排名小于等于k，挂到x上，类似于kth操作
	else y = id, split(lc[id], k, x, lc[id]);//如果当前节点的排名大于k，挂到y上
	pushup(id);
}

这样，如果你要分裂出 [l,r][l,r] 这个区间，你只需要这样：

1
2
3
4
int a, b, c;
split(root, r, b, c);//分裂[1,r]区间到b
split(b, l - 1, a, b);//在b中分裂[1,l-1]区间到a，b中剩余的就是[l,r]区间
//此时b区间就是[l,r]

合并时直接正常合并即可，不需要做任何更改。

1
2
3
4
5
6
7
8
9
10
inline int merge(int x, int y) {
	if(!x || !y)	return x + y;
	if(w[x] > w[y]) {
		pushdown(x), rc[x] = merge(rc[x], y), pushup(x);//合并前先下传标记
		return x;
	} else {
		pushdown(y), lc[y] = merge(x, lc[y]), pushup(y);
		return y;
	}
}

区间和

只需要先分裂出这个区间，然后输出即可。

1
2
3
4
5
6
7
8
inline long long query(int l, int r) {
	long long ret = 0;
	int a, b, c;
	split(root, r, b, c), split(b, l - 1, a, b);//分裂区间[l,r]到b
	ret = sum[b];//sum[b]即为[l,r]的区间和
	root = merge(a, merge(b, c));//别忘了合并回去
	return ret;
}

区间加

先分裂出这个区间，再打懒标记（别忘了修改这个节点的值）。

1
2
3
4
5
6
inline void modify(int l, int r, long long x) {
	int a, b, c;
	split(root, r, b, c), split(b, l - 1, a, b);//分裂区间[l,r]到b
	add[b] += x, val[b] += x;//打加法标记
	root = merge(a, merge(b, c));
}

插入和删除

这道题没有这两种操作，但是了解一下总是好的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void insert(int pos,int val) {
    int a, b;
    split(root, pos, a, b);
    root = merge(a, merge(newNode(val), b));
}
inline void erase(int pos) {//单点删除
    int a, b, c;
    split(root, pos-1, a, b),split(b, 1, b, c);
    root = merge(a, c);
}
inline void erase(int l, int r) {//区间删除
	int a, b, c;
	split(root, r, b, c), split(b, l - 1, a, b);
	root = merge(a, c);
}

完整代码

这样就做完了！

注意：这道题坑点很多，比如每个与值有关的变量都要long long，返回值也要long long。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <chrono>
#include <random>
using namespace std;
int root, len, lc[100010], rc[100010], sz[100010], w[100010];
long long val[100010], sum[100010], add[100010];
mt19937 mt(chrono::steady_clock::now().time_since_epoch().count());
inline int newNode(long long x) {
	++len, val[len] = sum[len] = x, lc[len] = rc[len] = add[len] = 0, sz[len] = 1, w[len] = mt();
	return len;
}
inline void pushup(int id) {
	sz[id] = sz[lc[id]] + sz[rc[id]] + 1;
	sum[id] = sum[lc[id]] + sum[rc[id]] + val[id];
}
inline void pushdown(int id) {
	if(!add[id])	return;
	if(lc[id])	val[lc[id]] += add[id], add[lc[id]] += add[id], sum[lc[id]] += sz[lc[id]] * add[id];
	if(rc[id])	val[rc[id]] += add[id], add[rc[id]] += add[id], sum[rc[id]] += sz[rc[id]] * add[id];
	add[id] = 0;
}
inline void split(int id, int k, int &x, int &y) {
	if(!id)	return x = y = 0, (void)0;
	pushdown(id);
	if(sz[lc[id]] + 1 <= k)	x = id, split(rc[id], k - sz[lc[id]] - 1, rc[id], y);
	else y = id, split(lc[id], k, x, lc[id]);
	pushup(id);
}
inline int merge(int x, int y) {
	if(!x || !y)	return x + y;
	if(w[x] > w[y]) {
		pushdown(x), rc[x] = merge(rc[x], y), pushup(x);
		return x;
	} else {
		pushdown(y), lc[y] = merge(x, lc[y]), pushup(y);
		return y;
	}
}
inline void modify(int l, int r, long long x) {
	int a, b, c;
	split(root, r, b, c), split(b, l - 1, a, b);
	add[b] += x, val[b] += x;
	root = merge(a, merge(b, c));
}
inline long long query(int l, int r) {
	long long ret = 0;
	int a, b, c;
	split(root, r, b, c), split(b, l - 1, a, b);
	ret = sum[b];
	root = merge(a, merge(b, c));
	return ret;
}
int n, m, op, l, r;
long long x;
int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i++)	cin >> x, root = merge(root, newNode(x));
	while(m--) {
		cin >> op >> l >> r;
		if(op == 1)	cin >> x, modify(l, r, x);
		else	cout << query(l, r) << endl;
	}
	return 0;
}

平衡树与线段树的优缺点

平衡树的优点：极其易背（无旋Treap只有两个关键函数，所有函数几乎都是对称的），可扩展性极强；

线段树的优点：效率相比平衡树较高（无旋Treap开O2 896ms，线段树不开O2 635ms）；代码较短。

数据结构
#平衡树 #数据结构 #讲义 #Splay
平衡树-2：平衡树与区间操作
https://www.d0j1a1701.cc/p/c7a0ecbe/
作者
d0j1a_1701
发布于
2022年1月20日
许可协议
CC-BY-SA